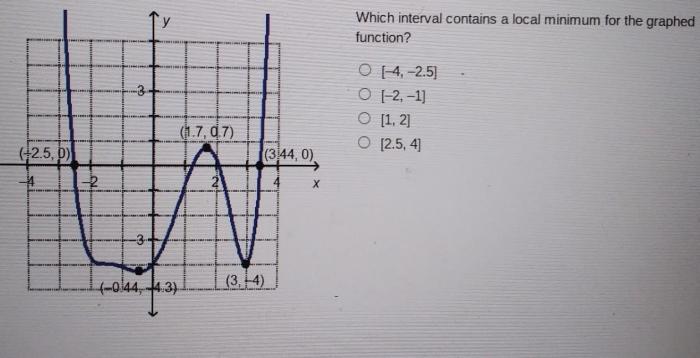
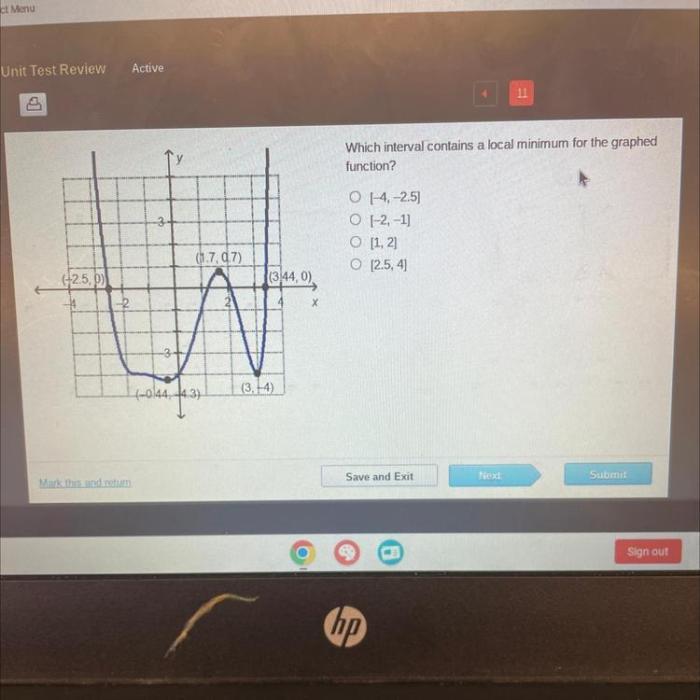
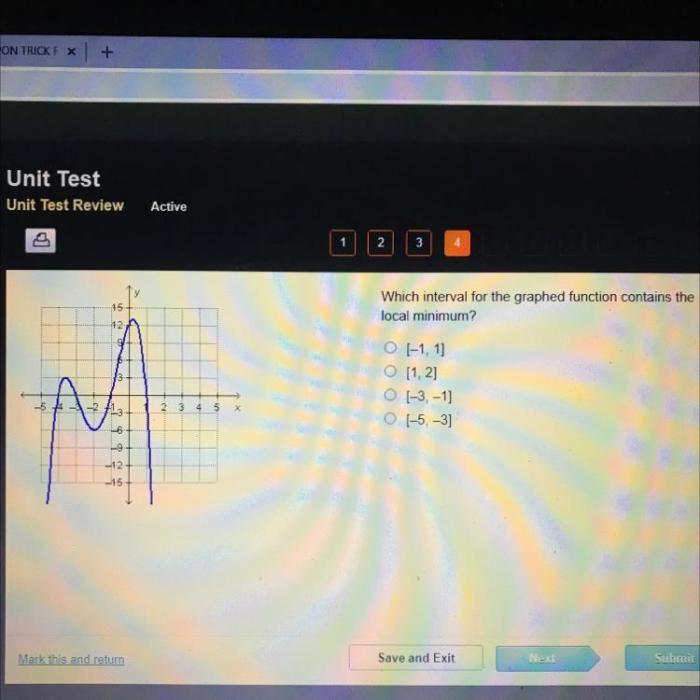
In the realm of calculus, determining which interval for the graphed function contains the local minimum is a fundamental concept that unlocks a deeper understanding of function behavior. This article delves into the intricacies of local minima, providing a comprehensive guide to identifying intervals that encompass these critical points.
By exploring the mathematical definition, graphical representation, and practical applications of local minima, we unravel the significance of this concept in various fields, including optimization and real-world problem-solving.
Definition of Local Minimum
A local minimum of a graphed function is a point where the function value is lower than the values at nearby points on the graph. Mathematically, a local minimum occurs at a point (x, f(x)) where f'(x) = 0 and f”(x) > 0. Examples of functions with local minima include quadratic functions, cubic functions, and exponential functions.
Identifying Local Minimums on a Graph
To identify local minima on a graph, find the critical points by setting the first derivative equal to zero. These critical points are potential local minima or maxima. Then, use the second derivative test to determine whether each critical point is a local minimum or maximum.
If f”(x) > 0 at a critical point, then that point is a local minimum.
Intervals Containing Local Minimums
An interval is a set of all numbers between two given numbers. To determine if an interval contains a local minimum, check if the function is decreasing on the interval to the left of the critical point and increasing on the interval to the right of the critical point.
Analyzing a Graphed Function for Intervals Containing Local Minimums: Which Interval For The Graphed Function Contains The Local Minimum
To analyze a graphed function for intervals containing local minima, follow these steps:
- Find the critical points by setting the first derivative equal to zero.
- Use the second derivative test to determine whether each critical point is a local minimum or maximum.
- For each local minimum, determine the interval on which the function is decreasing to the left and increasing to the right.
For example, consider the function f(x) = x^3 – 3x^2 + 2. The critical points are x = 0 and x = 2. The second derivative test shows that x = 0 is a local minimum. The function is decreasing on the interval (-∞, 0) and increasing on the interval (0, ∞), so the interval (-∞, 0) contains the local minimum.
Applications of Finding Intervals Containing Local Minimums
Finding intervals containing local minima has practical applications in optimization problems. For example, in manufacturing, finding the local minimum of a cost function can help determine the optimal production quantity that minimizes costs. In finance, finding the local minimum of a risk function can help investors choose the optimal portfolio that minimizes risk.
Expert Answers
What is the mathematical definition of a local minimum?
A local minimum of a function f(x) at a point c is a point where f(c) is less than or equal to f(x) for all x in some open interval containing c.
How do you identify local minima on a graph?
Local minima can be identified on a graph by locating points where the function changes from decreasing to increasing. This can be done by using the first derivative test, which involves finding the critical points of the function and determining the sign of the first derivative at those points.
What is the significance of finding intervals containing local minima?
Finding intervals containing local minima is important because it allows us to identify the regions of the function where the function is at its lowest value. This information can be used for optimization problems, such as finding the minimum value of a function on a given interval.