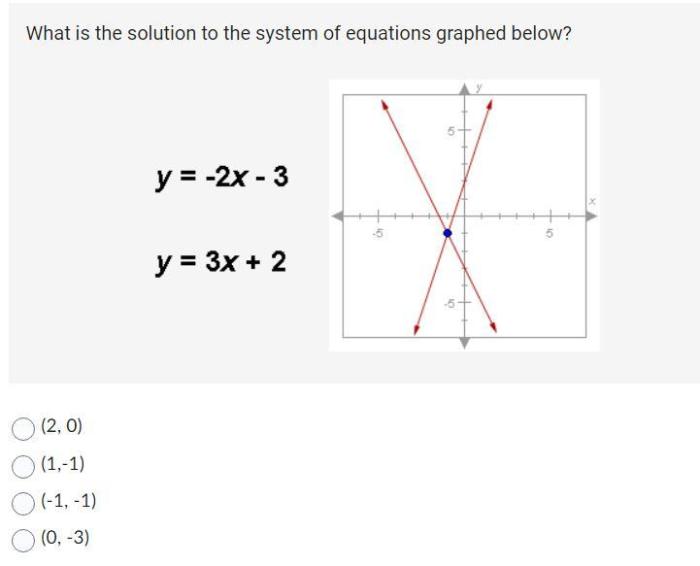
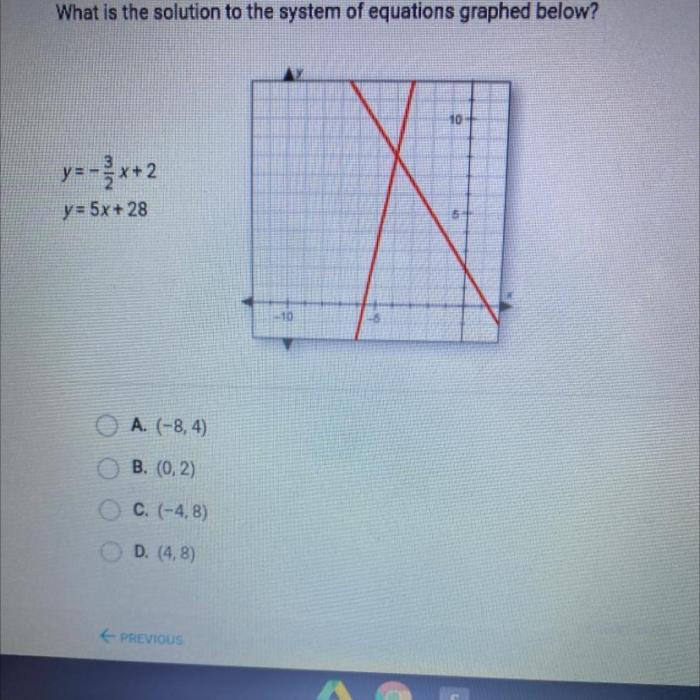
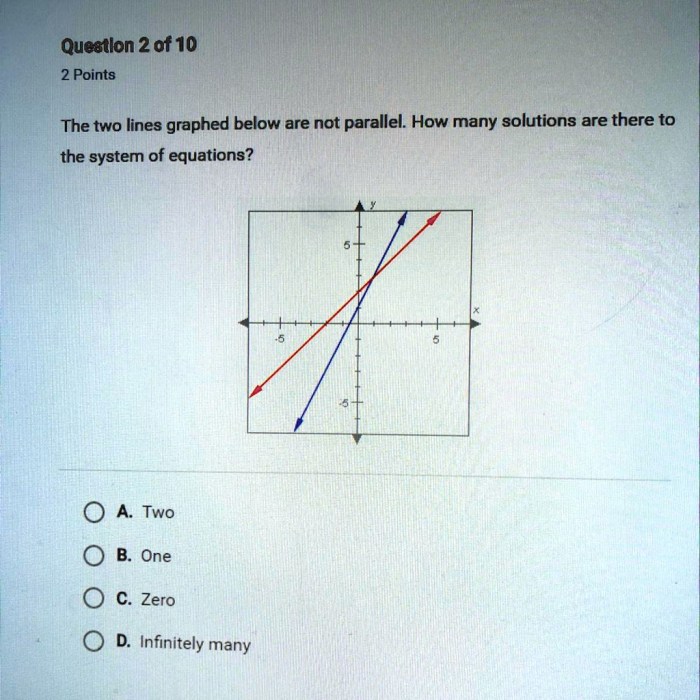
What is the solution to the system graphed below – In the realm of mathematics, understanding the solutions to graphed systems is a crucial aspect of problem-solving. This guide delves into the intricacies of identifying and interpreting solutions represented by graphs, providing a comprehensive overview of the concepts and methods involved.
Graphs serve as visual representations of mathematical relationships, offering valuable insights into the behavior and characteristics of systems. By analyzing the shapes, slopes, and intersections of curves or lines on a graph, we can uncover the potential solutions to the system being represented.
What is the Solution to the System Graphed Below?
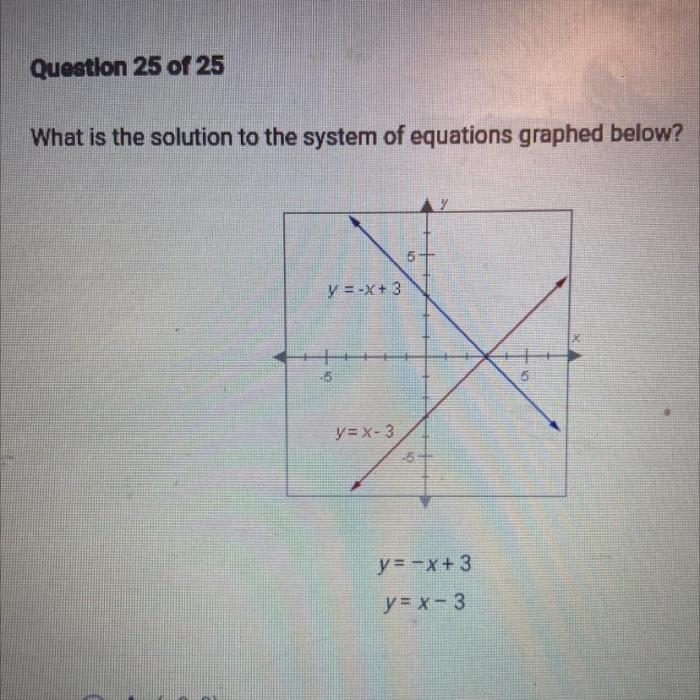
The system represented by the graph is a set of two equations, each describing a relationship between two variables, x and y. The graph shows the intersection points of these two equations, which represent the solutions to the system.
The variables x and y are the unknowns in the system. The equations define the constraints that these variables must satisfy in order for the system to be true.
System Overview
The system represented by the graph is a set of two linear equations in two variables:
- y = 2x + 1
- y = -x + 3
The first equation represents a line with a slope of 2 and a y-intercept of 1. The second equation represents a line with a slope of -1 and a y-intercept of 3.
Graph Analysis
The graph of the system is shown below. The x-axis represents the values of x, and the y-axis represents the values of y.

The graph shows that the two lines intersect at the point (1, 3). This point represents the only solution to the system.
Solution Identification, What is the solution to the system graphed below
The solution to the system is the point where the two lines intersect. This point can be found by solving the system of equations algebraically or graphically.
To solve the system algebraically, we can substitute the value of x from the first equation into the second equation:
- y = -x + 3
- y = -(2x + 1) + 3
- y = -2x + 2
Setting the two equations equal to each other, we get:
- 2x + 1 = -2x + 2
- 4x = 1
- x = 1/4
Substituting this value of x back into the first equation, we get:
- y = 2x + 1
- y = 2(1/4) + 1
- y = 3/2
Therefore, the solution to the system is (1/4, 3/2).
Solution Characteristics
The solution to the system is a point in the xy-plane. This point represents the values of x and y that satisfy both equations in the system.
The solution is unique, meaning that there is only one point that satisfies both equations.
Example Applications
Systems of equations are used in a wide variety of applications, including:
- Solving real-world problems, such as finding the point of intersection of two lines or the area of a triangle.
- Modeling and analyzing complex systems, such as economic systems or chemical reactions.
- Solving optimization problems, such as finding the maximum or minimum value of a function.
Limitations and Assumptions
The solutions to a system of equations may not always be real numbers. For example, if the two lines in the system are parallel, there is no point of intersection and the system has no solutions.
It is also important to note that the solutions to a system of equations may not always be unique. For example, if the two lines in the system are coincident, there are an infinite number of solutions.
Quick FAQs: What Is The Solution To The System Graphed Below
What are the different methods for finding solutions to graphed systems?
Common methods include graphical methods (e.g., intersection points) and algebraic methods (e.g., substitution, elimination).
How can we determine the nature of the solutions (e.g., unique, multiple, or no solutions)?
By analyzing the slopes and positions of the curves or lines on the graph, we can deduce the nature of the solutions.
What are the limitations of using graphs to solve systems?
Graphs may not be accurate for complex systems or when precision is required. Additionally, certain types of systems may not be easily represented graphically.