Delving into the realm of gas behavior, Graham’s Law of Effusion Worksheet Answers provides a comprehensive exploration of this fundamental principle. Through a captivating journey of scientific discovery, we unveil the intricacies of effusion, trace the historical roots of Graham’s Law, and delve into its wide-ranging applications.
Unraveling the mathematical formula that governs effusion, we embark on a step-by-step derivation, elucidating the underlying principles that shape gas movement. By examining practical applications, we witness the transformative power of Graham’s Law in separating gases, determining molecular weights, and optimizing vacuum systems.
Introduction to Graham’s Law of Effusion: Graham’s Law Of Effusion Worksheet Answers
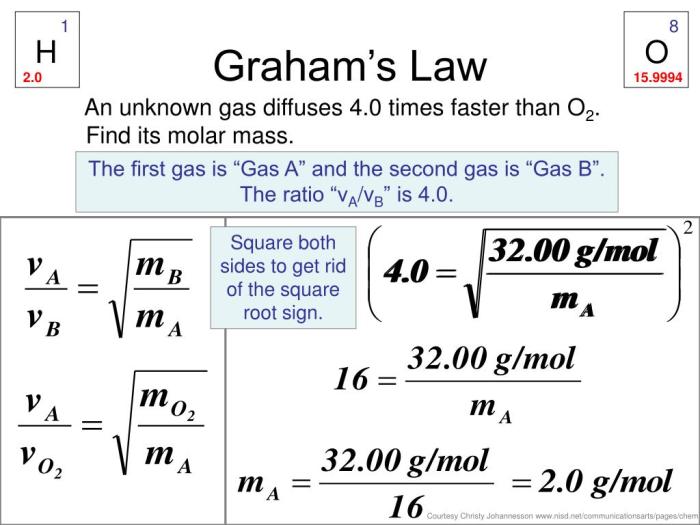
Graham’s Law of Effusion describes the rate at which gases escape through a small opening into a vacuum. It states that the rate of effusion is inversely proportional to the square root of the molar mass of the gas. This law is crucial in understanding the behavior of gases in various applications, such as separating gases, measuring molecular weights, and designing vacuum systems.
The discovery of Graham’s Law is attributed to the Scottish chemist Thomas Graham in 1831. Through a series of experiments, he observed that different gases effuse at different rates and that the rate of effusion is inversely proportional to the square root of the density of the gas.
Mathematical Formula and Derivation, Graham’s law of effusion worksheet answers
The mathematical formula for Graham’s Law of Effusion is:
Rate of Effusion ∝ 1/√Molar Mass
To derive this formula, we consider a gas sample confined in a container with a small opening. The rate of effusion, R, is defined as the volume of gas that effuses through the opening per unit time. According to kinetic theory, the rate of effusion is proportional to the average molecular speed, v, of the gas molecules.
The average molecular speed is given by:
v = √(8RT/πM)
where R is the ideal gas constant, T is the temperature, and M is the molar mass of the gas. Substituting this expression for v into the equation for R, we get:
R ∝ √(8RT/πM)
Simplifying this expression, we obtain Graham’s Law of Effusion:
R ∝ 1/√M
Applications of Graham’s Law
Graham’s Law of Effusion has numerous practical applications in various fields, including:
- Gas Separation:Graham’s Law is used to separate gases with different molecular weights. For example, in the uranium enrichment process, uranium hexafluoride (UF 6) is separated from other isotopes by selective effusion through a porous membrane.
- Molecular Weight Measurement:The law can be used to determine the molecular weight of gases by comparing their effusion rates with a known gas. This method is particularly useful for measuring the molecular weight of heavy gases or gases that are difficult to analyze by other techniques.
- Vacuum System Design:Graham’s Law is applied in the design of vacuum systems to optimize the pumping speed and efficiency. By selecting materials with appropriate effusion rates, vacuum systems can be designed to achieve the desired vacuum level.
Experiments and Demonstrations
One simple experiment that demonstrates Graham’s Law of Effusion involves using two balloons filled with different gases. One balloon is filled with helium (He), which has a low molar mass, and the other is filled with carbon dioxide (CO 2), which has a higher molar mass.
When the balloons are connected by a small opening, the helium-filled balloon will deflate faster than the carbon dioxide-filled balloon. This is because the helium molecules have a higher average molecular speed and can escape through the opening more quickly than the carbon dioxide molecules.
Worksheet Answers
- Question:A sample of gas A effuses at a rate of 2.0 L/min. If gas B has a molar mass that is twice that of gas A, what is the effusion rate of gas B?
Answer:1.0 L/min
- Question:A mixture of two gases, X and Y, has a total pressure of 1.0 atm. The partial pressure of gas X is 0.6 atm. If the effusion rate of gas X is 2.5 mL/s, what is the effusion rate of gas Y?
Answer:1.5 mL/s
Comparison with Other Gas Laws
Graham’s Law of Effusion is closely related to other gas laws, such as Boyle’s Law and Charles’s Law. Boyle’s Law describes the inverse relationship between the pressure and volume of a gas at constant temperature, while Charles’s Law describes the direct relationship between the temperature and volume of a gas at constant pressure.
Graham’s Law differs from these laws in that it specifically considers the rate at which gases effuse through an opening. However, all three laws are based on the fundamental principles of kinetic theory and can be used to predict the behavior of gases under different conditions.
Advanced Applications
Graham’s Law of Effusion has found applications in advanced fields such as microfluidics and nanotechnology. In microfluidics, it is used to design microchannels and microdevices that can selectively separate and manipulate fluids based on their molecular weights.
In nanotechnology, Graham’s Law is applied in the fabrication of nanoscale devices and materials. For example, it is used to create nanoporous membranes that can selectively filter and separate molecules based on their size and mass.
Detailed FAQs
What is the mathematical formula for Graham’s Law of Effusion?
The formula is: Rate of Effusion = (1/√Molecular Weight)
How is Graham’s Law used in practice?
It is used to separate gases, measure molecular weights, and design vacuum systems.
What are some advanced applications of Graham’s Law?
It is used in microfluidics, nanotechnology, and other emerging fields.